Задачи о библиотеке, максимальной площади прямоугольника и длине окружности Земли

"Книги признаться это самая моя большая страсть, затем идет музыка, природа, люди, творчество, а вообще меня интересуют люди, которые любят книги, музыку, природу, людей, имеют самовыражение."

Из мыслей Евгения Янкевича (Янжека)

Задача об библиотеке

Я решил признаться дурацкую задачу, как мне кажется, которую сам себе и поставил. А история вот в чем: Я на данный момент, конец марта 2023 года имею библиотеку из 743 книг, из нее я прочитал 344 и еще 56 прочитанных у меня сейчас нет в библиотеке, хотя я иногда покупаю прочитанные книги, которых у меня сейчас нет для библиотеки, чтобы были просто в библиотеке, мне это почему то нравится. И еще я узнал, что в среднем человек читает за жизнь 500 книг. Меня заинтересовал вопрос, при каком количестве прочитанных мною книг из библиотеки разность между прочитанных книг за жизнь в среднем у человека, а это 500 и прочитанных мною, обозначу это через у, будет равна  разности между большой долей от "Золотого сечения" книг у меня в библиотеке и книг прочитанных из нее. Мне показалось это красивым. Прочитанные книги из своей библиотеки я обозначил через х. Получаем два уравнения:

500-(х+56)=у

743*0.618-х=у

или

500-(х+56)=у

459-х=у

т.е.

х=459-у

и,

500-459+у-56=у

500-(459+56)+у=у

т.е. для решения этой системы нужно, чтобы:

500-(459+56)=0

где 459- это большая доля "Золотого сечения" от количества книг в библиотеке, а 56- это количество книг прочитанных, которых нет в библиотеке, обозначим количество книг в библиотеке как k, а количество книг прочитанных, которых нет в библиотеке как z, и получим систему уравнений:

500-(х+z)=y

k*0.618-x=y

откуда:

k=Ф(500-z)

z=500-1/Ф*k

при z=56, k=718, т.е. у меня многовато отсутствующих книг,

z при k=743 равно 41, т.е. нужно докупить 15 книг из числа прочитанных и отсутствующих в библиотеке,

при z=0, k=809,

а при k=0, z=500,

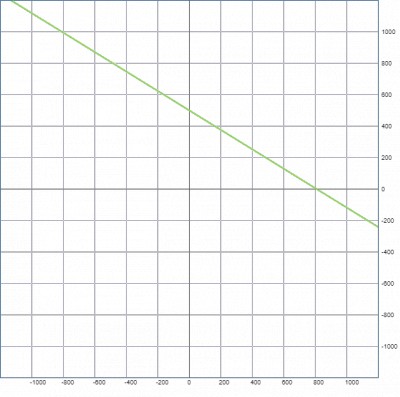
график z=500-0.618k

Как видим искомое равенство наблюдается только при библиотеке от 0 до 809 книг, остальное не имеет физического смысла.

Таблица для z=500-0.618k с шагом в 50 книг от 0 до 809:

z	500	469	438	407	376	345	315	284	253	222	191	160	129	98	67	37	6	0
k	0	50	100	150	200	250	300	350	400	450	500	550	600	650	700	750	800	809

Рассмотрим, какие же у нас будут х и у, при этих значениях, вспомнив что х<=k и получаем систему из трех уравнений:

500-(х+z)=y

k*0.618-x=y

х<=k

Возьмем k=500 книгам, тогда z=191 книга, х возьмем от 0 до 500, вот соответсвующая таблица для х и у:

у=500-191-х=-х+309 и второе уравнение аналогичное у=500*0.618-х=-х+309

у	309	259	209	159	109	59	9	0	не имеет смысла	не имеет смысла	не имеет смысла	не имеет смысла
х	0	50	100	150	200	250	300	309	350	400	450	500

т.е. диапазон прочитанных книг будет лежать от 0 до 309, а количество оставшихся для прочтения книг будет также лежать в диапазоне от 309 до 0, возможно прочитать и больше книг чем 309, прочтя например всю библиотеку, т.е. 500, но соотношение о равенстве оставшихся книг для прочтения уже не будет наблюдаться.

Задача о максимальной площади прямоугольника

Вспомнил я еще одну задачу, о которой читал еще учась в Новосибирском педагогическом в году так 1990-1992-ом, я когда-то очень любил матанализ и с удовольствием его изучал, задача о максимальной площади прямоугольника или участка, при заданной длине забора, т.е. длина одной стороны пусть х, другой у, их сумма а, а площадь S и имеем два уравнения:

х+у=а

х*у=S

и у=а-х

 х*(а-х)=S

итак S=-x²+a*x, исследуем эту функцию, ее первая производная S'=-2*x+a, вторая S''=-2, т.е. она выпукла вверх и она максимальна при S'=0 или: -2*х+а=0, х=а/2 и получаем что у=а/2, т.е. имеем квадрат, итак площадь максимальна при заданном периметре при равных сторонах или квадрате.

 

Задача Эрастофена о длине окружности Земли

Эрастофен (256-194 гг до н.э.), замечательный древнегреческий ученый, который вычислил длину окружности Земли, исходя из того, что, в день летнего солнцестояния в египетском городе Сиене, солнце находится прямо над головой и видно дно самого глубокого колодца, он измерил в этот день отклонение от веритикали тени в Александрии, между которыми было 800 км, и получил, что величина отклонения тени 7 градусов, итак попробуем и мы вычислить из этих условий длину окружности Земли, побудем немного Эрастофеном, таким образом получаем пропорцию: 7/360=800/Длина окружности Земли, отсюда Длина окружности Земли=800*360/7=41140 км. Что находится в пределах 10-15 процентов современных показателей окружности Земли.

Давайте в конце послушаем Долорес О'Риордан, ее Cranberries: