Идеальное дифференциальное уравнение

Я решил представить на суд публике идеальное дифференциальное уравнение, как я его понимаю, через Фидий, экспоненту и пи:

x''+Фx'=e^пи*t, или в числах x''+1.618x'=e^3.14t

его решение: x(t)=C₁-0.618*C₂e^-1.618t+0.0669e^3.14t или так представить: x(t)=C₁+Ф₂*C₂e^-Ф₁t+0.0669e^пи*t

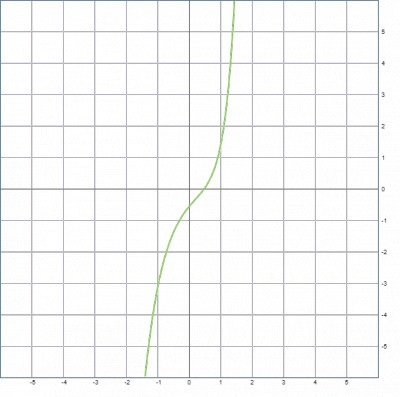
график, при С₁=0 и С₂=1: x(t)=-0.618e^-1.618t+0.0669e^3.14t или так представить: x(t)=Ф₂e^-Ф₁t+0.0669e^пи*t или предположить x(t)=Ф₂e^-Ф₁t-1/9*Ф₂e^пи*t

И получился "идеальный временной процесс", интересно имеется ли он в природе или технике? Пишите!

Подставим отрицательный Фидий, равный -0.618 в наше исходное уравнение: x''+Фx'=e^пи*t и получим: x''-0.618x'=e^3.14t

его решение: x(t)=C₁+1.618*C₂e^0.618t+0.1263e^3.14t или так представить: x(t)=C₁+Ф₁*C₂e^-Ф₂t+0.1263e^пи*t

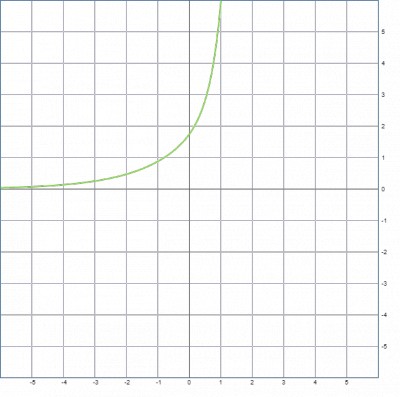
график, при С₁=0 и С₂=1: x(t)=1.618e^0.618t+0.1263e^3.14t или так представить: x(t)=Ф₁e^-Ф₂t+0.1263e^пи*t или предположить x(t)=Ф₁e^-Ф₂t+1/13*Ф₁e^пи*t

И получился еще один "идеальный временной процесс", снова интересно имеется ли его наличие в природе и технике ?

Да, вот еще, возьмем противоположные значения Ф: -1.618 и 0.618, и что же получим:

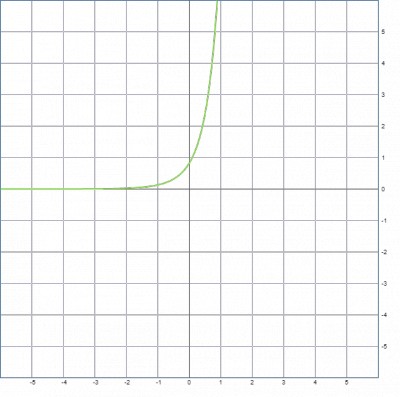
x''-1.618x'=e^3.14t , его решение: x(t)=С₁+0.618*C₂e^1.618t+0.2092*e^3.14t , график, при С₁=0 и С₂=1: x(t)=0.618e^1.618t+0.2092e^3.14t или так представить: x(t)=-Ф₂e^Ф₁t+0.2092e^пи*t или предположить x(t)=-Ф₂e^Ф₁t-1/3*Ф₂e^пи*t

И еще получился один "идеальный временной процесс", снова интересно имеется ли его наличие в природе и технике ?

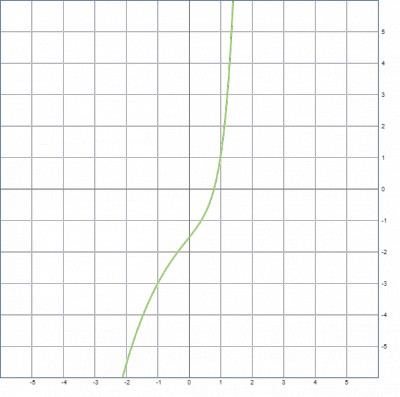
Рассмотрим x''+0.618x'=e^3.14t , его решение: x(t)=С₁-1.618*C₂e^-0.618t+0.0847e^3.14t, график, при С₁=0 и С₂=1: x(t)=-1.618e^-0.618t+0.0847e^3.14t или так представить: x(t)=-Ф₁e^Ф₂t+0.0847e^пи*t или предположить x(t)=-Ф₁e^Ф₂t+1/19*Ф₁e^пи*t

И наконец еще один "идеальный временной процесс", снова интересно имеется ли его наличие в природе и технике ?

Можно еще предположить существование идеального дифференциального уравнения n-го порядка:

x⁽ⁿ⁾+Ф^(n-1)x^(n-1)+...+Фx'=e^пи*t, его решения я не ищу, предоставляю это листателю сайта! Хотя возможно само уравнения не точно, это только первые наброски! Пишите, что у вас получилось?

Можно еще проанализировать уравнение: x⁽ⁿ⁾+Ф^(n-1)x^(n-1)+...+Фx'=0, т.е. без внешней нагрузки, свободные колебания системы? Тоже интересно! Например уравнение x''+Фx'=0?

Вообще, мне кажется, что общее уравнение не полное, не хватает члена х⁽⁰⁾, т.е. просто х, и тогда в общем виде получается:

x⁽ⁿ⁾+Фⁿx^(n-1)+Ф^(n-1)x^(n-2)+...+Ф³x^''+Ф²x'+Фх=e^пи*t

Получается, надо проанализировать решения следующих уравнений на идеальные временные процессы: x^''+Ф²x'+Фх=e^пи*t и x'+Фх=e^пи*t .Предлагаю это листателю сайта? Пишите, что у вас получилось! Я еще предполагаю наличие какого-то коэффициента перед e^пи*t  в уравнении?

Все это какие-то около художественно-мыслительные наброски! Весь мой сайт таков!

Напишу еще фантастическое идеальное дифференциальное уравнение, рассчитанное на 62-ричных, 38-компонентных числах Z₃₈⁶², отражающих значение функции по 62-мерному времени t₆₂, сбалансированное через 38-мерный Фидий Ф₃₈, и внешний процесс задается экспонентой (e₃₈⁶²)^(ПИ₃₈⁶²*t₆₂)

(Z₃₈⁶²)⁽ⁿ⁾+Ф₃₈ⁿ(Z₃₈⁶²)^(n-1)+...+Ф₃₈²(Z₃₈⁶²)'+Ф₃₈Z₃₈⁶²=(e₃₈⁶²)^(ПИ₃₈⁶²*t₆₂) , в общем такая заумь, сам дивлюсь! Какой там должен получиться в решении идеальный временной процесс, остается только догадываться и вообще какое это имеет отношение к нашей 4-х мерной реальности?

Давайте все же вернемся к нашим реалиям, возьмем размерность пространства равную пи, 3.14,  идеальную для жизни, как нам сообщили КОНовцы, тогда числа у нас будут 3.14-компонентные, и размерность времени равную экспоненте, е, 2.71, как я предположил, числа возьмем десятичные, к которым мы привыкли, уравнения рассмотрим первой и второй степени для простоты и их распространенности, итак получаем:

(Z_3.14)''+Ф_3.14²(Z_3.14)'+Ф_3.14Z_3.14=(e_3.14)^(ПИ_3.14*t_2.71)  и (Z_3.14)'+Ф_3.14Z_3.14=(e_3.14)^(ПИ_3.14*t_2.71)

И у нас получились идеальные дифференциальные уравнения для жизни, не много ни мало! Интересно было бы увидеть их решение, эти самые идеальные временные процессы для жизни?!

Послушайте в заключение замечательную композицию Metallica "Nothing else matters" в исполнении украинской группы B@B project: Бандура и Баян, и как же прекрасны сами исполнители:

И еще замечательную композицию ДиДюЛи "Путь домой":