Гармонические поверхности второго порядка

Это просто геометрическая зарисовка. Как мне кажется поверхности второго порядка будут гармоническими, если b/с=Ф=1.618, а a/b=Ф=1.618, и получаем:

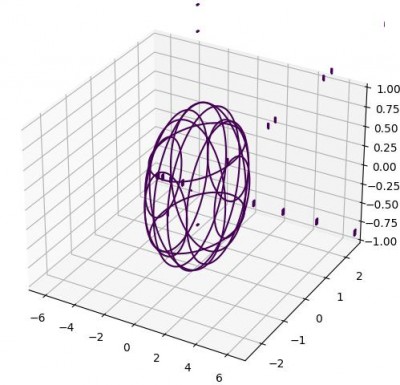
Эллипсоид: x^2/1.618^4+y^2/1.618^2+z^2/1=1, где xЕ(-1.618^4;1.618^4), yE(-1.618^2;1.618^2), zE(-1;1)

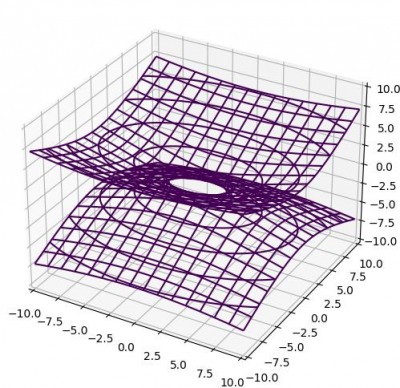
Гиперболоид: x^2/1.618^4+y^2/1.618^2-z^2/1=1, где xЕ(-10;10), yE(-10;10), zE(-10;10)

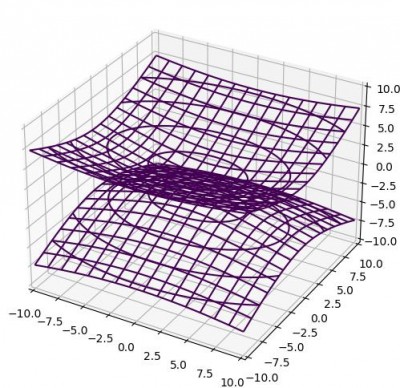
Двухполостный гиперболоид: x^2/1.618^4+y^2/1.618^2-z^2/1=-1, где xЕ(-10;10), yE(-10;10), zE(-10;10)

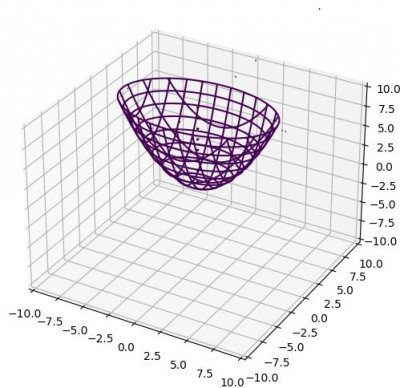
Эллиптический параболоид: x^2/1.618^2+y^2/1=2z, где xЕ(-10;10), yE(-10;10), zE(-10;10)

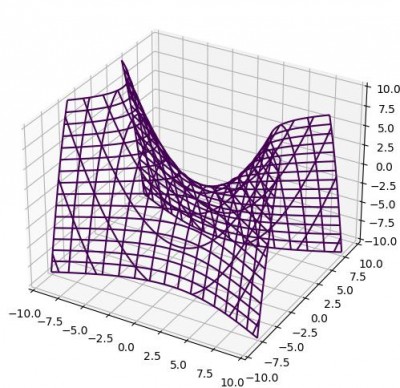
Гиперболический параболоид: x^2/1.618^2-y^2/1=2z, где xЕ(-10;10), yE(-10;10), zE(-10;10)

Давайте послушаем Чайф: